by jsendak | Apr 25, 2025 | GR & QC Articles
arXiv:2504.16156v1 Announce Type: new
Abstract: We study a point scalar charge in circular orbit around a topological star, a regular, horizonless soliton emerging from dimensional compactification of Einstein-Maxwell theory in five dimensions, which could describe qualitative properties of microstate geometries for astrophysical black holes. This is the first step towards studying extreme mass-ratio inspirals around these objects. We show that when the particle probes the spacetime close to the object, the scalar-wave flux deviates significantly from the corresponding black hole case. Furthermore, as the topological star approaches the black-hole limit, the inspiral can resonantly excite its long-lived modes, resulting in sharp features in the emitted flux. Although such resonances are too narrow to produce detectable dephasing, we estimate that a year-long inspiral down to the innermost stable circular orbit could accumulate a significant dephasing for most configurations relative to the black hole case. While a full parameter-estimation analysis is needed, the generically large deviations are likely to be within the sensitivity reach of future space-based gravitational-wave detectors.
Future Roadmap: Challenges and Opportunities
Introduction
In this article, we examine the conclusions of a study that investigates a point scalar charge in circular orbit around a topological star. This star is a regular, horizonless soliton that emerges from the dimensional compactification of Einstein-Maxwell theory in five dimensions. The findings of this study have implications for understanding astrophysical black holes and the possibility of extreme mass-ratio inspirals (EMRIs) around them. In this roadmap, we outline potential challenges and opportunities that lie ahead in this field of research.
Challenges
- Resonant Excitations: One significant challenge identified in the study is the resonant excitation of long-lived modes in the topological star as it approaches the black hole limit. This resonance leads to sharp features in the emitted flux, which deviates significantly from the flux in a black hole case. Understanding the dynamics and behavior of these resonances will require further investigation.
- Dephasing Analysis: To fully quantify the impact of the resonances on the emitted flux, a comprehensive parameter-estimation analysis is needed. This analysis will help determine the extent of dephasing that occurs during an inspiral down to the innermost stable circular orbit. Conducting such an analysis is a challenging task that requires a detailed understanding of the underlying physics and computational techniques.
Opportunities
- Detectability: Despite the challenges, the study suggests that the deviations caused by the resonant excitation and dephasing are likely to be within the sensitivity reach of future space-based gravitational-wave detectors. This presents an exciting opportunity to observe and analyze these effects, potentially providing insights into the nature of microstate geometries for astrophysical black holes.
- Parameter Variation: Extending the study to explore a wide range of parameter configurations is an opportunity for future research. By varying different parameters, such as the mass and charge of the scalar particle, and the properties of the topological star, a more comprehensive understanding of the system’s behavior can be gained.
Conclusion
In conclusion, the study of a point scalar charge in circular orbit around a topological star has highlighted both challenges and opportunities for future research in the field of extreme mass-ratio inspirals around astrophysical black holes. Overcoming challenges such as understanding resonant excitations and conducting dephasing analysis will pave the way for further investigation. The potential to detect and analyze these effects using future space-based gravitational-wave detectors provides an exciting opportunity to deepen our understanding of black hole microstate geometries. Exploring a broader parameter space will also contribute to a more comprehensive understanding of the system’s behavior. The road ahead holds great potential for uncovering new insights into the nature of black holes in our universe.
Read the original article

by jsendak | Nov 15, 2024 | GR & QC Articles
arXiv:2411.08921v1 Announce Type: new
Abstract: We construct equilibrium configurations for neutron stars using a specific $f(R,T)$ functional form, recently derived through gaussian process applied to measurements of the Hubble parameter. By construction, this functional form serves as an alternative explanation for cosmic acceleration, circumventing the cosmological constant problem. Here, we aim to examine its applicability within the stellar regime. In doing so, we seek to contribute to the modified gravity literature by applying the same functional form of a given gravity theory across highly distinct regimes. Our results demonstrate that equilibrium configurations of neutron stars can be obtained within this theory, with the energy density and maximum mass slightly exceeding those predicted by General Relativity. Additionally, we show that the value of some parameters in the $f(R,T)$ functional form must differ from those obtained in cosmological configurations, suggesting a potential scale-dependence for these parameters. We propose that further studies apply this functional form across different regimes to more thoroughly assess this possible dependence.
Summary: This article examines the applicability of a specific functional form of the $f(R,T)$ gravity theory, derived through gaussian process applied to measurements of the Hubble parameter, to equilibrium configurations of neutron stars. The results show that equilibrium configurations can be obtained within this theory, with slightly higher energy density and maximum mass compared to General Relativity. The study also suggests a potential scale-dependence for certain parameters in the functional form, indicating the need for further investigation across different regimes.
Introduction
The $f(R,T)$ functional form, derived through gaussian process applied to measurements of the Hubble parameter, provides an alternative explanation for cosmic acceleration and addresses the cosmological constant problem. This article aims to explore the applicability of this functional form within the stellar regime by studying equilibrium configurations of neutron stars.
Results
The study demonstrates that equilibrium configurations of neutron stars can be obtained within the $f(R,T)$ gravity theory. The energy density and maximum mass predicted by this theory slightly exceed those predicted by General Relativity. This suggests a potential modification to our understanding of gravity in the stellar regime.
Parameter Variation
The study also reveals that the values of certain parameters in the $f(R,T)$ functional form must differ from those obtained in cosmological configurations. This implies a potential scale-dependence of these parameters, which needs to be further investigated. Understanding the scale-dependence of these parameters is crucial for fully comprehending the implications of the $f(R,T)$ theory across different regimes.
Roadmap for Future Studies
- Further Studies: Future studies should apply the $f(R,T)$ functional form across different regimes to assess the potential scale-dependence of the theory’s parameters more thoroughly. This could involve examining other astrophysical objects, such as white dwarfs or black holes, to investigate whether the modifications observed in neutron stars are unique to this specific stellar regime.
- Parameter Exploration: Researchers should conduct extensive parameter exploration to determine the range of values that allow for consistent equilibrium configurations of neutron stars. This will help establish the validity of the $f(R,T)$ theory and refine our understanding of the scale-dependence of its parameters.
- Observational Tests: Observational tests should be designed to verify the predictions of the $f(R,T)$ theory in the stellar regime. This could involve comparing the observed properties of neutron stars with the theoretical predictions derived from the $f(R,T)$ functional form. Such observational tests will provide empirical evidence to support or refute the applicability of this theory.
Challenges and Opportunities
- Challenges: One of the main challenges is the complexity of the $f(R,T)$ theory, which requires careful parameterization and exploration. Additionally, obtaining observational data on neutron stars with sufficient accuracy and precision may pose a challenge.
- Opportunities: Successfully applying the $f(R,T)$ functional form across different regimes and validating its predictions would revolutionize our understanding of gravity. It could potentially lead to a unified theory of gravity that encompasses both cosmological and stellar phenomena. Furthermore, the potential scale-dependence of the theory’s parameters opens up avenues for new research and theoretical developments.
Conclusion
The results of this study demonstrate the viability of using the $f(R,T)$ functional form within the stellar regime to obtain equilibrium configurations of neutron stars. The slightly higher energy density and maximum mass compared to General Relativity indicate the need for further investigation into the scale-dependence of the theory’s parameters. Future studies should apply this functional form across different regimes, conduct parameter exploration, and design observational tests to fully assess the potential of the $f(R,T)$ theory and its implications for our understanding of gravity.
Read the original article

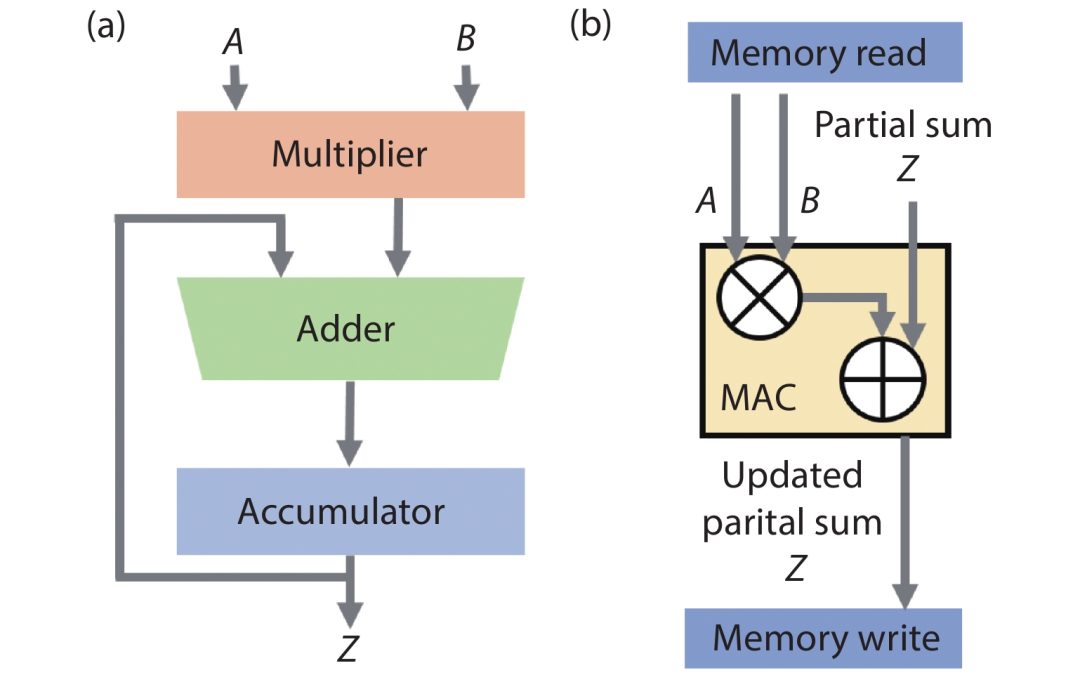
by jsendak | Apr 9, 2024 | Computer Science
Expert Commentary
In this article, the authors address one of the major challenges faced by CMOS devices at nanometer scale – increasing parameter variation due to manufacturing imperfections. Variability in process parameters can significantly affect the performance and reliability of circuits, as the nominal operating conditions may not be sufficient to overcome timing violations across the entire variability spectrum.
Traditionally, timing guardbands have been used to account for process variations, but this approach often leads to pessimistic estimates and performance degradation. To overcome this limitation, the authors propose a novel circuit-agnostic framework for generating variability-aware approximate circuits.
The key idea behind their approach is to accurately portray variability effects by creating variation-aware standard cell libraries. These libraries are fully compatible with standard Electronic Design Automation (EDA) tools, ensuring that the generated circuits can be seamlessly integrated into existing design flows.
The authors take a comprehensive approach by calibrating the underlying transistors against industrial measurements from Intel’s 14nm FinFET technology. This allows them to accurately capture the electrical characteristics of the transistors and incorporate the variability effects into their framework.
In their experiments, the authors explore the design space of approximate variability-aware designs to automatically generate circuits with reduced variability and increased performance, all without the need for timing guardbands. The results show that by introducing a negligible functional error of merely .3times 10^{-3}$, their variability-aware approximate circuits can reliably operate under process variations without sacrificing application performance.
This work is significant as it addresses a critical challenge in nanometer-scale CMOS design. As process technology continues to advance, process variations become more pronounced, and traditional design techniques may not be sufficient to mitigate their impact. The proposed framework provides a promising solution for incorporating variability-aware approximate computing principles into circuit design, enabling improved performance and reliability.
Future research in this area could focus on exploring different trade-offs between functional error and performance improvement. The authors have shown that a small functional error can lead to significant gains in performance, but it would be interesting to investigate the limits of this trade-off and identify the optimal balance for different applications.
Furthermore, extending this approach to more advanced process nodes and different technologies would be valuable. The authors have validated their framework using Intel’s 14nm FinFET technology, but assessing its effectiveness in other manufacturing processes, such as those based on nanosheet or nanowire transistors, would provide valuable insights into its scalability and applicability.
In conclusion, this work presents a novel framework for generating variability-aware approximate circuits that eliminate the need for timing guardbands. By accurately capturing process variations and incorporating them into the design process, the proposed approach offers improved performance and reliability in nanometer-scale CMOS designs.
Read the original article