“Addressing Inconsistent Pixel Area in Unprojected Raster Maps: Insights and Solutions”

It is well known, though often dismissed, that the areas of spatial units (cells, pixels) based on unprojected coordinates (longitude-latitude degrees, arc-minutes or arc-seconds) are wildly inconsistent across the globe. Towards the poles, as the longitude meridians approach each other, the actual ground width of the pixels sharply decreases. So, for non-tropical regions, the actual area covered by these pixels can be quite far from the nominal “approximately 1 km at the Equator” (or 10 km, etc.) which is often referred in biogeography and macroecology studies.

The function below combines several tools from the ‘terra’ R package to compute the (mean or centroid) pixel area for a given unprojected raster map. By default, it also produces a map illustrating the latitudinal variation in the pixel areas.

pixelArea <- function(r, # SpatRaster
                       type = "mean", # can also be "centroid"
                       unit = "m",  # can also be "km"
                       mask = TRUE,  # to consider only areas of non-NA pixels
                       map = TRUE) {
  # version 1.2 (23 Jan 2024)

  stopifnot(inherits(r, "SpatRaster"),
            type %in% c("mean", "centroid"))

  r_size <- terra::cellSize(r, unit = unit, mask = mask)
  if (map) terra::plot(r_size, main = paste0("Pixel area (", unit, "2)"))
  areas <- terra::values(r_size, mat = FALSE, dataframe = FALSE, na.rm = FALSE)  # na.rm must be FALSE for areas[centr_pix] to be correct

  if (type == "mean") {
    cat(paste0("Mean pixel area (", unit, "2):n"))
    return(mean(areas, na.rm = TRUE))
  }

  if (type == "centroid") {
    r_pol <- terra::as.polygons(r * 0, aggregate = TRUE)
    centr <- terra::centroids(r_pol)
    if (map) {
      if (!mask) terra::plot(r_pol, lwd = 0.2, add = TRUE)
      terra::plot(centr, pch = 4, col = "blue", add = TRUE)
    }

    centr_pix <- terra::cellFromXY(r, terra::crds(centr))
    cat(paste0("Centroid pixel area (", unit, "2):n"))
    return(areas[centr_pix])
  }
}

Here’s a usage example for a central European country:

elev_switz <- geodata::elevation_30s("Switzerland", path = tempdir())
terra::plot(elev_switz)

terra::res(elev_switz)
# 0.008333333 degree resolution
# i.e. half arc-minute, or 30 arc-seconds (1/60/2)
# "approx. 1 km at the Equator"

pixelArea(elev_switz, unit = "km")
# Mean pixel area (km2):
# [1] 0.5892033

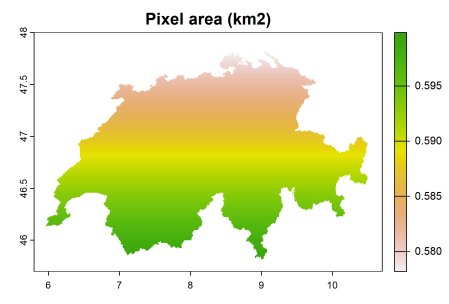
As you can see, pixel area here is quite different from 1 squared km, and Switzerland isn’t even one of the northernmost countries. So, when using unprojected rasters (e.g. WorldClim, CHELSA climate, Bio-ORACLE, MARSPEC and so many others) in your analysis, consider choosing the spatial resolution that most closely matches the resolution that you want in your study region, rather than the resolution at the Equator when this is actually far away. This was done e.g. in this paper (see Supplementary Files – ExtendedMethods.docx).

You can read more details about geographic areas in the help file of the terra::expanse() function. Feedback welcome!

Continue reading: Actual pixel sizes of unprojected raster maps

Considerations and Implications of Inconsistent Pixel Area in Unprojected Maps

The primary proposition in the article is the inconsistency of pixel area in geographic studies and models based on unprojected coordinates, such as longitude and latitude degrees, or arc-seconds and arc-minutes. This issue becomes more pronounced towards the poles as longitude meridians converge. Consequently, the actual ground coverage by each pixel decreases sharply, creating a significant difference between the nominal pixel area, usually referred to as “approximately 1 km at the Equator”, and the actual pixel area.

R’s ‘terra’ Package as a Solution

A potential solution to this problem, as proposed in the article, entails using specific tools from R’s ‘terra’ package. Users can calculate the average or centroid pixel area of an unprojected raster map, emphasizing the variations in pixel areas across latitude. This adjustment can lead to a more accurate representation of spatial data, particularly in non-tropical regions where the discrepancy is most noticeable.

Long-term Implications

In the long run, acknowledging and addressing this inconsistency could lead to significantly improved accuracy in macroecological and biogeographical studies. These enhanced insights could inform more effective conservation strategies and predictive modelling initiatives.

Future Developments

Given the rapid advancements in technology and geospatial analysis tools, it’s reasonable to expect further progress in addressing issues related to unprojected raster maps. Enhanced algorithms for calculating pixel area could lead to even more precise spatial representations. Also, it’s possible that machine learning technologies could be developed to automatically adjust for these discrepancies during data processing.

Actionable Advice

1. Adjust Pixel Calculation: If your work involves unprojected raster maps, especially involving non-tropical latitudes, consider incorporating tools that calculate the actual pixel area rather than relying on the nominal approximation.
2. Keep Updated: Stay informed about updates and improvements to geospatial analysis tools and consider integrating them into your work when they become available.
3. Collaborate: Consider collaborating with technologists focused on machine learning and AI. Their expertise could support the development of automated systems that can address pixel area inconsistencies.

Understanding and addressing the inconsistency of pixel area in raster maps based on unprojected coordinates is crucial in garnering accurate insights in macroecological and biogeographical studies. It is beneficial to leverage geospatial analysis tools which calculate the actual pixel area, and stay abreast with further developments in this field.

Read the original article