Want to share your content on R-bloggers? click here if you have a blog, or here if you don’t.
Flip a fair coin 100 times, resulting in a sequence of heads (H) and tails (T). For each HH in the sequence, Alice gets a point; for each HT, Bob does, so e.g. for the subsequence THHHT Alice gets 2 points and Bob gets 1 point. Who is most likely to win?
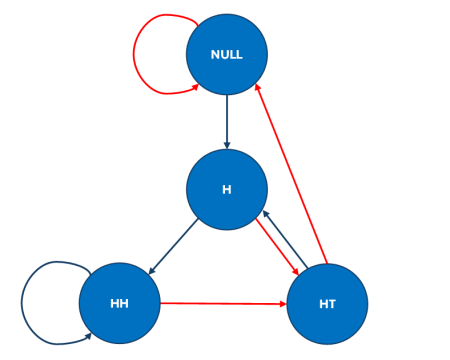
An interesting conundrum in that the joint distribution of (A,B) need be considered for showing that Bob is more likely. Indeed, looking at the marginals does not help since the probability of the base events is the same. A solution on X validated (for a question posted when the Fiddler’s puzzle came out, Friday morn) demonstrates via a four state Markov chain representation the result (obvious from a quick simulation) that Alice wins 45% of the time while Bob wins 48%. The intuition is that, each time Alice wins at least a point, Bob gets an extra point at the end of the sequence (except possibly at the stopping time t=100), while in other cases Alice and Bob have the same probability to win one point.
R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you’re looking to post or find an R/data-science job.
Want to share your content on R-bloggers? click here if you have a blog, or here if you don’t.
Continue reading: joint fiddlin
Understanding Coin Flip Probability Through a Markov Chain
The main thesis of the original text revolves around a question: If a fair coin is flipped 100 times, resulting in a sequence of heads (H) and tails (T), who out of Alice and Bob is more likely to win based on specific point gaining conditions? If each HH (two consecutive heads) sequence in the coin flips gives Alice a point, while each HT (head followed by a tail) sequence gives Bob a point, the joint distribution of Alice and Bob’s scores needs to be considered to determine the winner. This is a fascinating method to analyze probability distributions in sequences that might seem to provide even chances to both participants.
Key Points from the Discussion
- Equal probability of base events i.e. HT and HH in sequences doesn’t help to determine the most likely winner.
- A four-state Markov chain representation demonstrates that Alice is likely to win 45% of the time, whereas Bob has a winning likelihood of 48% with the rest of 7% being a tie.
- While Bob only scores when a HT sequence is encountered, he has a higher chance due to Alice ‘winning’ the point at the end of the sequence, except at the stopping time t=100.
Long-term Implications and Future Developments
The implications of this probability exercise are broader than it first appears. It encourages us to consider that not all sequences with an equal probability of base events have the same outcome and that the context of the sequence can drastically change the end result.
On a broader scale, this can be applicable to a wide range of scenarios, including pattern recognition in machine learning, economic forecasting models, or even situations in sports where the result of a game isn’t just determined by the likelihood of scoring but the sequence in which the scores occur.
Future study and progression can be directed towards understanding multi-state sequences beyond two and explore how these probabilities can change based on the scoring conditions and sequence length. Also, exploring situations where the base events do not have equal probabilities can provide more fascinating insights.
Actionable Advice
Developers and researchers working in data science, machine learning, or any field relying on probabilistic outcomes can leverage these insights to develop more nuanced models of prediction. Understanding that the order of events can change the overall probability, even when core event probabilities are equal, can lead to greater accuracy in models and predictions when applying these principles.
Also, continuing to learn and adapt machine learning algorithms is advisable as this kind of four-state Markov chain representation can be applied to a variety of fields to enhance precision in predictive models. Finally, bringing in inter-disciplinary experts for a broad explanation and understanding of these chains can also prove beneficial.