Sampling without replacement with unequal probabilities

Not proportional to w

A week ago I was surprised to read on Thomas Lumley’s Biased and Inefficient blog that when using R’s sample() function without replacement and with unequal probabilities of individual units being sampled:

“What R currently has is sequential sampling: if you give it a set of priorities w it will sample an element with probability proportional to w from the population, remove it from the population, then sample with probability proportional to w from the remaining elements, and so on. This is useful, but a lot of people don’t realise that the probability of element i being sampled is not proportional to w_i”

This surprised me profoundly – in the way that Bertrand Russell once wrote of surprise in some epistemological context of getting to the bottom of the stairs and finding there was one more stair to go than you unconsciously expected. That is, I hadn’t even been consciously aware of assuming that the probability of an element being sampled is proportional to the weight given to it, but if I had been asked if this was the case I would have given the wrong answer (‘yes’).

So I didn’t know this, but I should have.

Thomas had some examples in his blog relating to streams of data but I wanted to see for myself. So I wrote a function to simulate sampling from a small, finite population, with equal or unequal weights. So mostly, I sampled 10 units at a time from a population of 20; and gave them weights from about 0.005 to 0.095 ( a big range). The weights are forced to add up to 1 so they can be easily compared with that element’s proportion of the eventual sample of samples. And then I take some thousands of these samples of 10, and look at the proportion of the total collection that is each element.

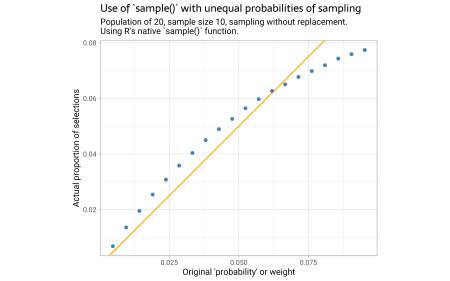
In the charts the follow, the brown diagonal line would be where the eventual proportion of element i being sampled is proportional to its weight. First, here is the main situation of concern – unequal weights, sampling without replacement, sample size is quite a big proportion of the population (10 out of 20):

OK! so we see the elements with low weights get sampled a bit more than naively expected, and the elements with high weights a bit less.

Just to check I’m not dreaming, here’s the same simulation but this time we are sampling with replacement. Now, everything works as intuitively might be expected, the eventual proportion in our sample of samples is exactly matched to the original weights:

Here’s the code for that function and those two runs of it.

library(tidyverse)
library(glue)

compare_ppswor <- function(n = 10,
                           N = 20,
                           replace = FALSE,
                           reps = 1e5,
                           prob = 1:N / sum(1:N),
                           FUN = sample){

  x <- paste0("unit", 1:N)
  x <- factor(x, levels = x)
  prob <- prob / sum(prob)


  samples <- lapply(rep(n, reps), function(size){
    FUN(x, size = size, prob = prob, replace = replace)
    })

  s <- ifelse(replace, 'with replacement', 'without replacement')
  m <- case_when(identical(FUN, sample) ~ "R's native `sample()` function.",
                 identical(FUN, sample_unequal) ~ "experimental function based on Brewer (1975).",
                 identical(FUN, sample_brewer) ~ "Brewer (1975) as implemented by Tillé/Matei.")

  p <- tibble(
    original = prob,
    selected = as.numeric(table(unlist(samples))) / (reps * n)
  )  |>
    ggplot(aes(x = original, y = selected)) +
    geom_abline(slope = 1 , intercept = 0, colour = "orange") +
    geom_point(colour = "steelblue") +
    labs(x = "Original 'probability' or weight",
         y = "Actual proportion of selections",
         subtitle = glue("Population of {N}, sample size {n}, sampling {s}.nUsing {m}"),
         title = "Use of `sample()` with unequal probabilities of sampling") +
    coord_equal()

  return(p)
}

compare_ppswor()
compare_ppswor(replace = TRUE)

When the sample is a smaller proportion of a population, the no-replacement discrepancy is less, as seen in these examples with population sizes of 50 and 250.

At the extreme, if the sample size is the same size as the population (20 each in the simulation below), then of course, all samples without replacement are identical to the population, so it is impossible for the end proportion to be anything other than 1/N each:

Brewer’s 1975 algorithm

Thomas was writing because there are plans to change this behaviour of sample(), or at least add an option to change it, so instead the eventual proportion of samples containing an element will be proportional to the weight even when sampling with unequal probabilities and without replacement. The method that is going to be implemented in R (written in C of course before being hooked into R – it’s an inherently iterative thing that will only be efficient in compiled code) is based on a method published way back in 1975 by Ken Brewer.

An aside – I had the privilege and pleasure to be taught sampling by Professor Brewer back in the 1990s at the Australian National Universitiy – at least it was a pleasure at the time (sheer entertainment value as well as the pleasure of witnessing someone who was a virtuoso in the subject matter, master of the theory of sampling), and I now belatedly realise what a privilege it was. I do think he struggled occasionally with some of the students though; one of my vivid memories of my whole education at ANU was of him in confusion when one of the less mathematically inclined asked him to explain what an equation taking up a fair proportion of the blackboard “means” – “Means? means? it means what it says!”

I don’t have easy access to the 1975 paper but I found this very interesting question relating to it on Cross-Validated. From that discussion and reading the part of the SAS manual referred to, it sounds like SAS implements the algorithm only for when the sample in a given strata is 2, but Brewer had generalised his method to larger samples. The answer given by the ever-reliable StasK seems pretty clear on how this is done, so presuming he got it right I had a go at implementing this method into R, with code below in the form of two functions P() and sample_unequal():

#' @param p probabilities of remaining units
#' @param n total sample size
#' @param k which sequence of the sample this is for the sampling of
P <- function(p, n, k){
  r <- n - k + 1
  D <- sum((p * (1 - p)) / (1 - r * p))
  new_p <- p * (1 - p) / (D * (1 - r * p))
  return(new_p)
}

sample_unequal <- function(x, size, prob, replace = FALSE, keep = FALSE){

  if(size > length(x)){
    stop("Sample size cannot be larger than the population of units")
  }

  if(replace){
    stop("Only sampling without replacement implemented at this point")
  }

  if(size > (1 / max(prob))){
    stop(glue("Sample size ({size}) cannot be larger than 1 / max(prob) (which is {1 / max(prob)})"))
  }

  d <- tibble(x, prob)

  the_sample <- x[NULL]
  remnants <- x
  remnant_p <- prob

  for(k in 1:size){
    new_p <- P(remnant_p, size, k)

    if(keep){
      d2 <- tibble(x = remnants, prob = new_p)
      names(d2)[2] <- paste0("k", k)
      d <- d |>
        left_join(d2, by = "x")
    }

    if(min(new_p) < 0){
      warning("Some negative probabilities returned")
      new_p <- pmax(0, new_p)
    }

    latest_sample <- sample(remnants, size = 1, prob = new_p)
    which_chosen <- which(remnants == latest_sample)
    remnants <- remnants[-which_chosen]
    remnant_p <- remnant_p[-which_chosen]
    the_sample <- c(the_sample, latest_sample)

      }

  if(keep){
    return(list(the_sample = the_sample, d = d))
  } else {
    return(the_sample)
  }
}  

I’m not guaranteeing I got it right – feedback is welcome.

Of course, I designed this to be plugged into my function I made earlier for comparing eventual sample proportions to the weights given, so with compare_ppswor(FUN = sample_unequal, reps = 10000) I can get this comparison:

Interestingly, it’s still not exactly ‘right’ in the sense that the eventual proportions in the sample aren’t exactly those given in the form of weights. But it’s much better at doing this than the current sample() method is.

And if we have a sample that is say 25% of the population instead of 50% with compare_ppswor(n = 5, FUN = sample_unequal, reps = 10000), then we get results where the proportions and weights are pretty indistinguishable:

OK that’s all. I played around with this a bit more, particularly trying to understand the limitations on the algorithm which breaks down as the sample size gets bigger in relation to the population, but none of it was really interesting enough to write up. A full script with a bit more in it is available in the source code for this blog.

I guess the meta-lesson is to watch out for things you’re assuming without noticing you are.

Late addition!

When I posted about this on Mastodon, Thomas Lumley drew my attention to the sampling library by Yves Tillé and Alina Matei, which contains multiple algorithms for sampling with unequal probabilities without replacement. I hadn’t even stopped to look because really this was about me learning, but yes, of course there’s an R package for that. So I wrapped their UPbrewer function in a little function to work with my comparison. Unlike me they had read Brewer’s actual article, and their implementation of course works perfectly:

So the version I hacked together based on a Cross-Validated answer clearly doesn’t do justice to the method proposed by Brewer (or more likely was some other method he proposed separately).

For the record here’s the little convenience function to test the Tillé/Matei implementation:

#--------------using sampling library------------------
library(sampling)
sample_brewer <- function(x, size, prob, replace = FALSE, keep = FALSE){
 pik <- prob / sum(prob) * size
 s <- UPbrewer(pik)
 the_sample <- x[which(s == 1)]
 return(the_sample)
 }

compare_ppswor(FUN = sample_brewer, reps = 10000)

I’ts much faster too!

Continue reading: Sampling without replacement with unequal probabilities by @ellis2013nz

Key Points

In the text, the author emphasizes different mechanisms of sampling in R, specifically focusing on the sample() function without replacement and with unequal probabilities of individual units. This leads to sequential sampling, which most people misunderstand as being proportional to the weight assigned to the element (w). Unexpectedly, the actual probability of an element being sampled isn’t proportional to w.

The author utilized a function to simulate sampling, either with equal or unequal weights, to validate the assertion made by Thomas Lumley. The results showed a discrepancy between sampled elements with low weights and those with high weights, which were sampled more and less than expected, respectively. Interestingly, this discrepancy was not present when sampling was done with replacement. The author then extends their experiment to when the sample is a smaller proportion of a population and found that the no-replacement discrepancy is less.

The text further details plans to modify the behavior of the R’s sample(), aiming for a proportional relationship between the eventual sample proportion and the weight assigned, even when sampling with unequal probabilities without replacement. This modification draws from an algorithm published by Ken Brewer in 1975.

Long-term Implications and Future Developments

The author testifies an implementation of this method in R, which though not ‘right’ to precision, is better than the current sample() method at approximating sample proportions to the assigned weights. There is a plan to implement Brewer’s 1975 algorithm into R which means that this work can have long-term implications in the accuracy and efficiency of sampling in R.

The results of these changes may lead to richer and more accurate analysis and research done using R. The planned change to the sample() function will be a better implementation than the current system and will provide more accurate results to the variations in assigned weights. The introduction of the Tillé/Matei implementation into R also shows promise in delivering perfect results.

Actionable Advice

An important takeaway from the findings presented by the author is the need to accurately understand the mechanisms of the R functions we use. Often, functions are used without a clear understanding of their exact operation or output, and this can lead to skewed or misinterpreted results.

Another critical suggestion is to always simulate and validate any assumptions you may have regarding the operation of a function. By thoroughly testing these assumptions, you’ll be better informed about the actual operations, potentially overcoming any unexpected surprises or discrepancies that may arise.

Remember to stay aware of updates to R’s libraries and algorithms, as developers are continuously working to improve R’s capabilities. Always stay open to testing and adopting these changes in your work.

Lastly, developers who work extensively with R or similar programming languages should consider implementing newer technologies like Brewer’s 1975 algorithm into their work. While nothing is perfect, it is always advantageous to use best and more recent technologies which tend towards a more precise approximation of reality.

Read the original article